In machine learning, regularization is a method by which the ML model cost/error function is changed, to include an extra variable called the regularization hyperparameter. There are two basic types of regularization: L1-norm (lasso regression) and L2-norm (ridge regression).
The Lasso regularization uses the L1 norm parameter. The lasso regularized cost function is calculated as shown below.
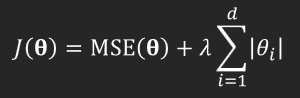
Lasso regression is applied to MSE cost function, where:
- J(θ) is the cost function itself, now with regularization term applied.
- MSE(θ) is the cost function before regularization.
- λ is the regularization hyperparameter.
- d is the total length of θ.
- θi is a model parameter.
The Ridge regression regularization uses the L2 norm parameter. The ridge regression regularized cost function is calculated as shown below.
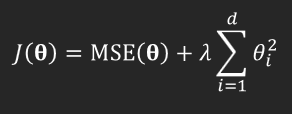
Ridge regression is applied to MSE cost function, where:
- J(θ) is the cost function MSE itself, now with regularization term applied.
- MSE(θ) is the cost function before regularization.
- λ is the regularization hyperparameter.
- d is the total length of θ.
- θi is a model parameter.
We also have the elastic net regression regularization method, which combines the best of both the above regularization methods and adds a weight to each of the lasso and ridge regression methods, to stress one or the other (or balance them).
Regularization differs from normalization and standardization, in that regularization aims to solve the problem of ML model overfitting, when there is a lot of noise in the dataset.
Comparing gradient descent with regularization
Gradient descent and its variations are internal optimization methods for regression algorithms, whereas regularization is mostly a method to tackle the overfitting problem by applying a penalizing hyperparameter in the ML algorithm cost function. Regularization is primarily used to overcome the overfitting problem, whereas gradient descent can be used in all sorts of regression scenarios. Regularization methods (L1, L2) are generally used with gradient descent optimization. A good analysis of gradient descent optimization and L1/L2 regularization methods can be found at: https://neptune.ai/blog/fighting-overfitting-with-l1-or-l2-regularization.